Projektowanie przypadków testowych w oparciu o wyjściowe klasy równoważności

Nie jest to popularne podejście, natomiast może okazać się bardzo użyteczne w pewnych warunkach oraz ułatwić projektowanie przypadków testowych.

Wyjściowe klasy równoważności w testowaniu

Podział danych wejściowych (lub wyjściowych) na klasy równoważności to jedna z technik projektowania przypadków testowych. Klasa równoważności w testowaniu to zbiór danych o analogicznym sposobie przetwarzania przez oprogramowanie, używana zwykle do przeprowadzenia testu. Tak sformułowana definicja zakłada, że wspomniane klasy muszą być rozłączne.

Wyróżniamy następujące klasy równoważności:

1. poprawne (pozytywne) - zbiór danych wejściowych, dla którego system zachowa się w poprawny sposób. Innymi słowy, wprowadzone dane zostaną przyjęte oraz przetworzone bez błędów,
2. niepoprawne (negatywne) - zbiór danych wejściowych, który testowany moduł lub system powinien odrzucić.

Projektując klasy równoważności, należy zadbać o to, aby:

1. cała dziedzina została pokryta klasami,
2. każdy argument został przypisany dokładnie do jednej klasy – warunek konieczny dla poprawnie zaprojektowanych klas równoważności.

Pojęcie klas równoważności w testowaniu można stosować zarówno do danych wejściowych, jak i danych (wartości) wyjściowych. Wyjściowe klasy równoważności to koncepcja, w której dzielimy możliwe dane wyjściowe na grupy (klasy) na podstawie określonych kryteriów. Wyjściowe klasy równoważności odnoszą się do klasyfikacji wartości testowanej funkcjonalności, które oprogramowanie generuje w odpowiedzi na przekazane dane wejściowe. Zgodnie z definicją wyjściowych klas możemy stwierdzić, że:

1. Pomiędzy klasami wejściowymi oraz wyjściowymi zachodzi relacja równoważności (relacja znana z matematyki). Oznacza to, że w projektowaniu przypadków testowych nie ma znaczenia czy dzielimy wartości testowanej metody na zbiory rozłączne, czy dzielimy argumenty wejściowe na zbiory rozłączne. Ważne tylko jest to, aby podział ten był poprawny.
2. Może również zaistnieć sytuacja, gdy pewna klasa równoważności da się dodatkowo podzielić na mniejsze klasy rozłączne – co zostanie pokazane na przykładach w dalszej części artykułu.

Projektując wyjściowe klasy równoważności, należy również zadbać o to, aby cały zbiór wartości wyjściowych został pokryty wspomnianymi klasami. Aby wykazać prawdziwość stwierdzenia z podpunktu (a) wprowadzimy pewne definicje, a następnie przeprowadzimy dowód.

Niech f będzie testowaną funkcją. Niech X będzie zbiorem argumentów tej funkcji, a X' zbiorem wartości, czyli f(X) = X'

Def. Mówimy, że pomiędzy elementami zbioru X zachodzi relacja równoważności R, jeżeli

1. xRx, relacja jest zwrotna,
2. xRy=>yRx, relacja jest symetryczna,
3. xRy,yRz=>xRz, relacja jest przechodnia,

gdzie x,y,z ∈ X.

Def. Niech  X będzie zbiorem, na którym określono relację równoważności ∼.R.  Klasą równoważności lub klasą abstrakcji (także warstwą) elementu  x∈ X nazywa się zbiór:

[x]_R  = {y ∈X; yRx},

czyli zbiór wszystkich elementów zbioru X równoważnych z elementem x w sensie relacji R. Jeżeli relacja równoważności znana jest z kontekstu, ukazywane jest to zwykle jako [x]. Z definicji klas równoważności wynika wprost, że są one rozłączne.

Wniosek 1. Podział danych testowych na rozłączne klasy o analogicznym przetwarzaniu jest relacją równoważności. 

Wniosek 2. Pomiędzy wejściowymi klasami równoważności a klasami wyjściowymi zachodzi relacja równoważności. Wobec tego, przypadki testowe projektowane w oparciu o podział danych wejściowych są równoważne przypadkom wejściowym, projektowanym w oparciu o dane wyjściowe.

Dowód. 

1) Najpierw wykażemy, że dwa różne elementy z różnych klas wejściowych nie mogą należeć do jednej klasy wyjściowej w wyniku działaniu funkcji f.

Niech [x] oraz [y] będą dwoma rozłącznymi klasami wejściowymi oraz niech

f(x)= x’,f(y)= y’.

Załóżmy, że x’R'y’. Jeżeli wyjściowa klasa równoważności jest poprawna, to wtedy zachodzi warunek: 

[x]=[y],

czyli

xRy,

co oznacza  sprzeczność z założeniem, że [x] oraz [y] są  rozłącznymi klasami.

2) Teraz wykażemy,  że jeżeli  ~(x’R'y’), to [x]≠[y], gdzie [x'],[y^' ] są poprawnie zdefiniowanymi rozłącznymi klasami równoważności na wyjściu.

Załóżmy, że [x]=[y].  Wtedy  xRy, co oznacza, że [x']=[y'],  a to jest sprzeczne z założeniem. 

Biorąc pod uwagę 1) oraz 2) wykazaliśmy, że przypadki testowe projektowane w oparciu o podział danych wejściowych są równoważne przypadkom wejściowym projektowanym w oparciu o dane wyjściowe.

Biorąc pod uwagę 1) oraz 2) wykazaliśmy, prawdziwość stwierdzenia (a). 

Kiedy warto stosować technikę projektowania testów opartą o wyjściowe klasy równoważności?

• Podział danych na klasy równoważności “zwalnia” testera z obowiązku sprawdzania ogromnej ilości kombinacji danych, co w praktyce jest awykonalne (jedna z siedmiu podstawowych zasad testowania),
• Jeżeli liczba klas równoważności na wyjściu testowanej funkcji jest stosunkowo niewielka, wtedy można się skupić na tym, by najpierw zaprojektować podstawowe ścieżki w oparciu o zachowanie na wyjściu, a w drugim kroku dobrać dane na wejściu.

Przykład zastosowania wyjściowych klas równoważności

Załóżmy, że mamy dwie aplikacje: Trigger oraz Service. Trigger komunikuje się z aplikacją Service za pomocą REST API oraz wyzwala pewne funkcje zaimplementowane w aplikacji Service. Trigger zawiera zestaw procesów mogących na wejściu przyjmować różne argumenty. Celem testów jest integracja pomiędzy wspomnianymi aplikacjami. Wywołanie dowolnej metody za pomocą REST API  może zakończyć się sukcesem lub niepowodzeniem. Niepowodzenie może skutkować błędem w aplikacji lub kodem wskazującym na błąd. Wspomniana integracja może zostać zaprezentowana za pomocą schematu:

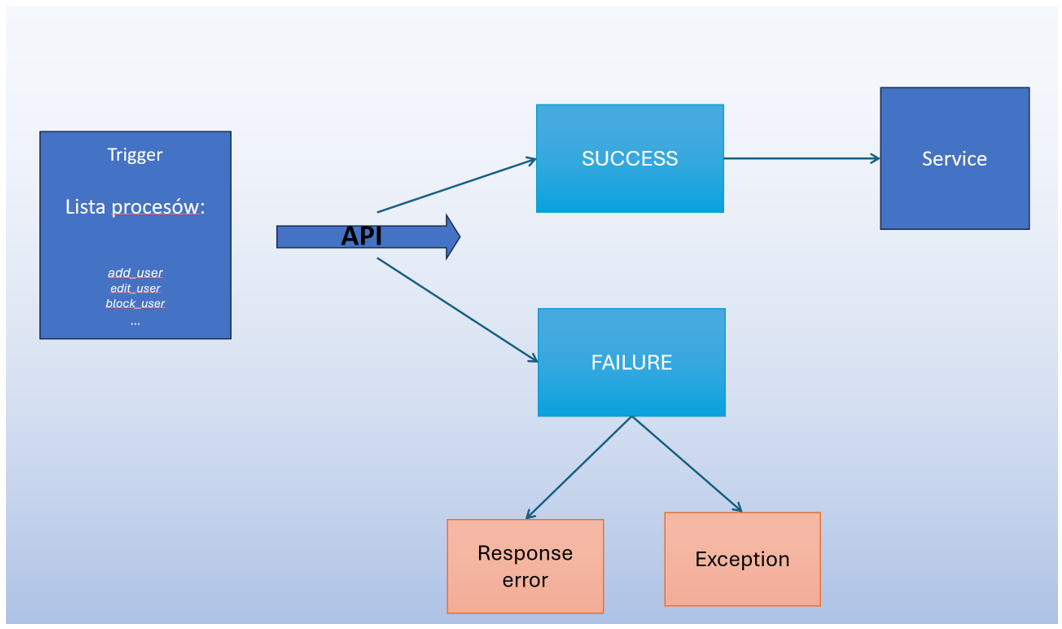Testowane funkcje mogą na ogół przyjmować kilka parametrów, na dodatek liczba możliwych wartości wejściowych jest bardzo duża. Z podstaw testowania wiadomo, że gruntowne testowanie jest niemożliwe. Możemy wówczas zacząć projektować testy tak, aby osiągnąć konkretny wynik na wyjściu. Załóżmy, że metoda add_user przyjmuje takie dane wejściowe jak:

• Imię, 
• Nazwisko,
• PESEL,
• Miejscowość zamieszkania
• Nr domu/mieszkania

Numer PESEL musi być wartością unikalną, składającą się z 11 cyfr. Wszystkie wymienione argumenty są obowiązkowe. Liczba kombinacji wartości wejściowych jest niemożliwa do przetestowania w rozsądnym czasie. Patrząc na wyjście funkcji add_user wiadomo, że w aplikacji Service użytkownik może, lecz nie musi zostać utworzony. Wobec tego mamy dwa pierwsze przypadki testowe:

1. Utworzenie użytkownika
2. Próba utworzenia użytkownika zakończona niepowodzeniem.

Niepowodzenie testu może przejawiać się na kilka sposobów:

1. Podanie nr PESEL, który już istnieje (405, method not allowed),
2. Podanie liczby cyfr różnej od 11 (422, unprocessable entity),
3. Brak wymaganych argumentów lub puste argumenty (400, bad request)
4. Niepoprawne dane wejściowe (400, bad request)
5. Niepoprawnie zdefiniowane ciało testowanej metody (exception)

W rozdziale 2 wspomnieliśmy o tym, że klasa równoważności może dać się dodatkowo podzielić na mniejsze klasy rozłączne. Testowanie negatywne metody add_user wprowadza taki właśnie podział. Klasa z odpowiedziami 400 może zostać podzielona na dwa mniejsze podzbiory:

• brak wymaganych argumentów lub puste argumenty,
• niepoprawne dane wejściowe. 

Zaprojektowane podczas analizy przypadki testowe (dla metody add_user) mogą zostać pokazane  za pomocą schematu umieszczonego niżej na obrazku. Minimalna liczba przypadków, wśród których każda klasa wyjściowa jest pokryta dokładnie jeden raz, jest równa liczbie prostokątów, z których nie wychodzi żadna strzałka. W naszym przykładzie ta liczba jest równa 6:

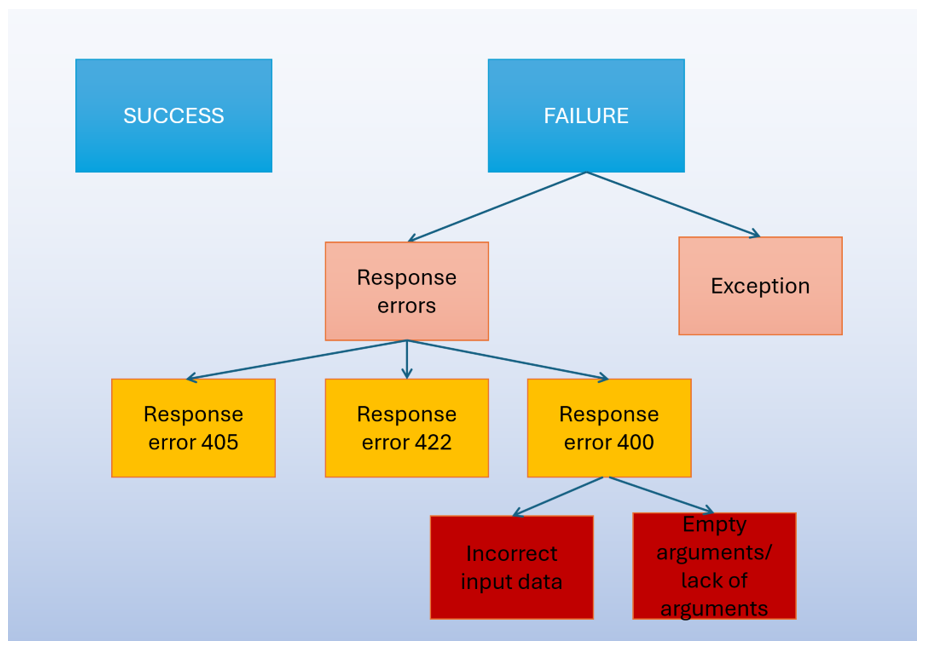W ten sposób można podejść do projektowania testów integracji pomiędzy dowolnymi systemami informatycznymi. Analizując to, co może stać się na wyjściu danej metody, mamy “za darmo” zaprojektowaną minimalną liczbę przypadków testowych. 

Podsumowanie

Artykuł został napisany w celu zaprezentowania czytelnikowi, jak można użyć techniki wyjściowych klas równoważności podczas projektowania przypadków testowych. Istnieją sytuacje, w których kombinacja danych wejściowych jest tak duża, że nie jesteśmy w stanie przetestować wszystkich możliwości. Nic nie stoi jednak na przeszkodzie, aby analizować wyjście testowanej funkcjonalności. W pewnych sytuacjach (np. testowanie API) ta technika zmniejsza ilość wygenerowanych przypadków tak, aby pokryte zostały wszystkie możliwe zachowania testowanej metody, co z kolei daje nam możliwość przeprowadzenia testów w rozsądnym czasie.