Pairwise testing: projektowanie przypadków testowych i testy konfiguracji metodą redukcji par danych wejściowych

1. Wstęp

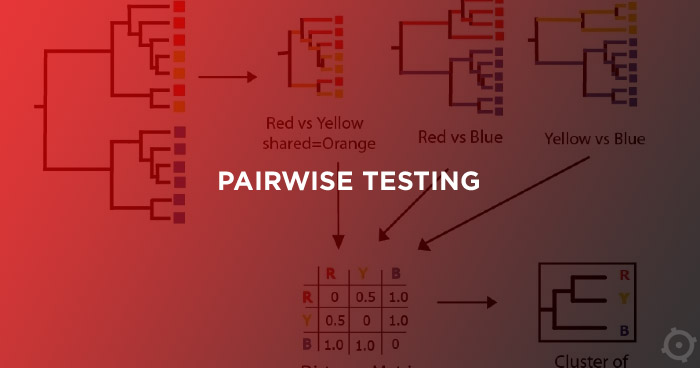
Testowanie par (ang. Pairwise testing): Czarnoskrzynkowa technika projektowania przypadków testowych w której przypadki testowe są projektowane tak, aby wykonać wszystkie możliwe dyskretne kombinacje każdej pary parametrów wejściowych. Jest wiele metod i algorytmów, które rozwiązują zagadnienie testowania parami. Powstało sporo prac naukowych, dotyczących tego zagadnienia. W przedstawionym artykule skupimy się na tym, aby miał on jak największą wartość dla testerów oraz tych ludzi, którzy projektują przypadki testowe. 

2. Testy kombinatoryczne

Testy kombinatoryczne to problem przed którym stoimy, gdy mamy produkt, który przetwarza wiele zmiennych, które mogą wchodzić w interakcje. Zmienne mogą pochodzić z różnych źródeł, np. interfejsu użytkownika, systemu operacyjnego, urządzeń peryferyjnych, bazy danych, lub w sieci. Celem analizy kombinatorycznej jest potwierdzenie, że różne kombinacje zmiennych są prawidłowo obsługiwane przez system lub wykrycie defektów, które są wynikiem kombinacji par zmiennych w konfiguracji lub par zmiennych wejściowych. W wielu przypadkach zdarza się, że wystąpienie awarii jest związane z kombinacją dwóch parametrów, a nie ich większej ilości. Więc takie podejście podczas testów ma duży sens.

Testowanie parami zwykle zaczynamy wybierając wartości zmiennych wejściowych systemu. Wartości te są następnie przesuwane tak, aby  uzyskać pokrycie wszystkich par. Najczęściej wykorzystuje się do tego celu tablice ortogonalne (ang. Orthogonal Arrays, używane do eksperymentów statystycznych) lub pewne algorytmy ewolucyjne (rozwiązujące problemy optymalizacji). W artykule skupimy się głównie na reprezentacji konfiguracji za pomocą tablic.

Tablica ortogonalna to 2-wymiarowa tablica wybrana ze zbioru predefiniowanych tablic, opartych o kombinacje pewnej liczby zmiennych i zakresu wartości tych zmiennych. Każda zmienna reprezentuje kolumnę, a każda wartość tej zmiennej pojawia się w tablicy wielokrotnie. Ilość wierszy odpowiada liczbie przypadków testowych potrzebnych do pokrycia każdej pary kombinacji wartości dwóch zmiennych. 

3. Przykłady zastosowania metody pairwise testing

Przypuśćmy teraz, że mamy do przetestowania system S, który ma trzy wejścia:

Załóżmy, że zbiór D = X×Y×Z, jest iloczynem kartezjańskim danych wejściowych, gdzie  

D(X)= {1,2},D(Y)= {Q,R},D(Z)= {5,6}.

Liczba przypadków testowych potrzebnych do przetestowania wszystkich kombinacji wynosi

2×2×2=8.

Ale, stosując metodę pairwise testing ograniczymy liczbę przypadków do 4, tak jak w tabeli poniżej:

Tabela 1: Przypadki testowe wygenerowane metodą pairwise testing dla systemu S 

W dalszej części artykułu zostanie wyjaśnione poprawne dobranie przypadków testowych.

Testowanie parami jest silnie związane z  matematyczną postacią tabeli 2-wymiarowej, czyli wspomnianej wcześniej tablicy ortogonalnej. Ta tablica ma specyficzne właściwości: 

• jest prostokątna,
• każda kolumna posiada nazwą zmiennej lub parametru.

Wartości dla każdej zmiennej pochodzą z pewnego zbioru nazwanego alfabetem. Alfabet dla każdej zmiennej nie musi składać się z liter – jest to kwestia umowna jakie symbole są elementami alfabetu. Konkretna wartość, reprezentowana przez symbol w alfabecie, który  jest formalnie zwany poziomem.

Wyobraźmy sobie teraz tabelę zawierającą kombinacje ustawień wyświetlania, systemów operacyjnych i drukarek. Jedna kolumna reprezentuje rozdzielczości ekranu 800 x 600 lub niska; 1024 x 768 lub średnia, oraz 1600 x 1200, wysoka. Druga kolumna reprezentuje systemy operacyjne Windows Vista, Windows 7 i Windows 8.1,  trzecia kolumna reprezentuje typy drukarek PostScript, LaserJet oraz Bubblejet. Chcąc przetestować każdy system operacyjny na każdej rozdzielczości ekranu, każdą drukarkę z każdym systemem operacyjnym  oraz każdą rozdzielczość  wyświetlacza z każdą drukarką, musielibyśmy mieć  tabelę z 3 x 3 x 3=27 wierszami. Pisząc te wszystkie opcje możemy użyć skrótów. Wszystko czego potrzebujemy to legenda lub mapowanie do każdej zmiennej powiązanej z literą alfabetu:

Niska = A, Średna = B, Wysoka = C; Windows Vista =A,  Windows 7 - B,  Windows 8.1 = C; PostScript = A, LaserJet = B, Bubblejet =C.

Niżej przedstawione są początkowe  wiersze w tabeli ortogonalnej, związanej z naszym przykładem:

W przypadku, gdy zdarzy się, że jeden z alfabetów będzie miał inną liczbę elementów niż pozostałe, to niektóre pary się powtórzą podczas testów. Jeśli będziemy chcieli zastosować podejście pairwise testing dobrze jest zacząć rozpisywać tabelę od zmiennej, która ma największą ilość elementów. W powtarzające się pary w innych kolumnach możemy wstawić symbol  np. * lub po prostu wpisać powtórzone wartości. Poniższy przykład ilustruje sytuację, w której poszczególne wejścia mają różną ilość danych wejściowych:

Załóżmy, że mamy do przetestowanie konfigurację systemu P, które posiada 3 wejścia 

X={A,B,C},Y={0,1},Z = {T,F}.

Wszystkie możliwe kombinacje systemu możemy przedstawić w tabeli:

 

Tabela 5: Wszystkie przypadki testowe systemu P

 

Otrzymujemy 12 przypadków testowych jednak możemy tutaj zastosować metodę pairwise testing w taki sposób, żeby mieć nie powtarzające się połączenia par X i Y ale również tak żeby dla każdego elementu z alfabetu X istniały dwa elementy z alfabetu Z. Wtedy nasza tabela będzie miała postać:

 

Tabela 6: Wszystkie przypadki testowe systemu P po redukcji metodą pairwise testing

 

Po redukcji otrzymujemy 6 przypadków kombinacji danych wejściowych lub konfiguracji.

4. Dlaczego warto stosować metodę pair wise testing?

W 1998 roku zostało opublikowane twierdzenie „No Free Lunch”. Mówi ono, że każda strategia rozwiązująca pewne problemy jest średnio taka sama dla wszystkich problemów (w tym optymalizacyjnych). To twierdzenie ma swój matematyczny dowód, więc jest prawdziwe i istnieje w każdych klasach problemów. Ale okazuje się, że po przyjęciu pewnych założeń pewna strategii jest najlepsze dla określonej klasy problemów. Jeśli popatrzymy na to twierdzenie pod kątem testów, to od razu widać, że istnieje ono w problemie optymalizacji i doboru przypadków testowych. Metoda pairwise testing stosowana mądrze z pewnością znajdzie swoje zastosowanie w pewnych problemach związanych z testowaniem.

Przetestowanie całej  konfiguracji na ogół nie jest możliwe. Warto więc znać tą metodę. Podstawową zaletą pairwise testing jest redukcja przypadków testowych, zmniejszenie czasu testów a przez to również kosztów związanych z testowaniem.

5. Kiedy metoda pairwise testing nie działa?

Nie jest prawdą, że pairwise testing „wykryje” każdą nieprawidłową implementację kodu.  Przypadki w których ta metoda może zawieźć to:

a) wybranie niepoprawnych wartości do testów,

b) brak odpowiedniej wyroczni testowej,

c) redukcja do par, które mają bardzo małe prawdopodobieństwo wystąpienia,

d) brak wiedzy na temat interakcji między danymi wyjściowymi.

 

6. Wnioski i uwagi

Testowanie parami znacząca zmniejsza liczbę przypadków testowych, dostarcza informacje o poprawności zaimplementowania konfiguracji par, znajduje błędy w kombinacji par, znajduje defekty mogące wystąpić przy dwóch zmiennych, a nie tylko przy jednej, natomiast brak defektów może być potwierdzeniem jakości oprogramowania.  Istnieją algorytmy oraz programy, które mają zaimplementowaną omawianą metodę, dzięki czemu nie trzeba tego robić ręcznie. 

Krytyczne myślenie i analiza empiryczna daje nam do zrozumienia, że znacząco spada liczba kombinacji, ale nie musi spadać w takim samym tempie liczba potrzebnych przypadków testowych. Jedno jest pewne: osoba, która stosuje metodę pairwise testing powinna mieć odpowiednią wiedzę i doświadczenie. W przeciwnym przypadku metoda może być nieskuteczna.

7. Dodatek. Pairwise testing: Framework i algorytmy. 

W przypadku, gdy mamy do czynienia z małą ilością parametrów , to stosowanie tablic ortogonalnych jest dobrym rozwiązaniem. Ale w przypadku, gdy tych parametrów jest np. 6 i każdy ma tylko wartości logiczne, to liczba konfiguracji jest równa 2⁶=64. W takim przypadku stosowanie tablicy będzie bardzo uciążliwe, dlatego warto wspomóc się oprogramowaniem, lub napisać własne. Popularną strategią jest strategia IPO.

7.1 Strategia IPO (In-Parameter-Order)

Załóżmy, że pewien system S ma parametry p₁,p₂,…,p_n, gdzie n ≥ 2. Niech T będzie zbiorem zawierającym kombinację par dla systemu S. Uproszczony framework, który opisuje strategię IPO, można przedstawić następująco:

 

 

Wyżej pokazana strategia (framework), zawiera zwroty poziomy przyrost oraz pionowy przyrost. Te nazwy, to nazwy algorytmów. Algorytm poziomy przyrost rozszerza zbiór testów T dodając wartość nowego parametru konfiguracyjnego do istniejących. Natomiast algorytm pionowy przyrost sprawdza, czy testy z nową wartością właściwie pokrywają nasz i modyfikuje testy tak, aby było ich możliwie jak najmniej oraz tak, aby pojawiły się w nich wszystkie wartości dodawanego parametru. Schemat tych dwóch algorytmów użytkownik znajdzie w pozycji [1] z bibliografii.

Bibliografia:

[1] A test generation strategy for pairwise testing, K. Tai and Y. Lei, IEEE 2002,

[2] In parameters order: A test generation strategy for pairwise testing, Y. Lei, K. Tai, IEEE 1998, 

[3] Pairwise Testing: A Best Practice That Isn’t, J. Bach, P. Schroeder,  testingeducation.org.